●謎の八卦(2)
・
・
・
・
・
*********************************
彡彡人ミミ 彡彡彡彡彡
| ⌒ ⌒ | MM ⌒ ⌒ MM
q 0―0 MMMMM ∩ ∩ MM m
(″ ▽ M ⌒ ⌒ M″ v ゛)/ ̄)
凸/Σ▽乃q ・ ・ p ̄Σ▽乃 ̄` /
\ /(″ ▽ ゛)\ 厂 ̄偶
===○=======○====================
子育て最前線の育児論byはやし浩司 12月 19日号
================================
━━━━━━━━━━━━━━━━━━¬¬¬¬¬――――――――――――――
★★★★★★★★★★HTML版★★★★★★★★★★★
マガジンを、カラー版でお楽しみください。(↓)をクリック!
http://bwhayashi2.fc2web.com/page023.html
★メルマガ(6万3000誌)の中で、2008年度、メルマガ・オブ・ザ・イヤーに
選ばれました!
★2009年、2010年、連続、カテゴリー部門・人気NO.1に選ばれました。
【1】(子育てのこと)□□□□□□□□□□□□□□□□□□□□□□□□□□□□
休みます。
【2】(特集)□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□□
●今日の目標
今日は、「八卦とDNA」について、もう一度、その謎解きに挑戦してみたい。
もし八卦と、DNA言語が一致していたら……。
これは世界の科学の常識をひっくり返すほどの大発見となる。
では、このつづきは、またあとで……。
2011/11/15朝記
Hiroshi Hayashi++++++Nov. 2011++++++はやし浩司・林浩司
●謎の八卦(易経)
+++++++++++++++++++++++++
今日は1日、八卦(易経)とDNAの関係について考えてみた。
何度も図表を見ながら、その向こうに隠された関係を
考えてみた。
(……関係があれば……という条件つきだが。)
が、意外と簡単に、謎解きの糸口をつかむことができた。
それを今日は、わかりやすく説明してみたい。
+++++++++++++++++++++++++
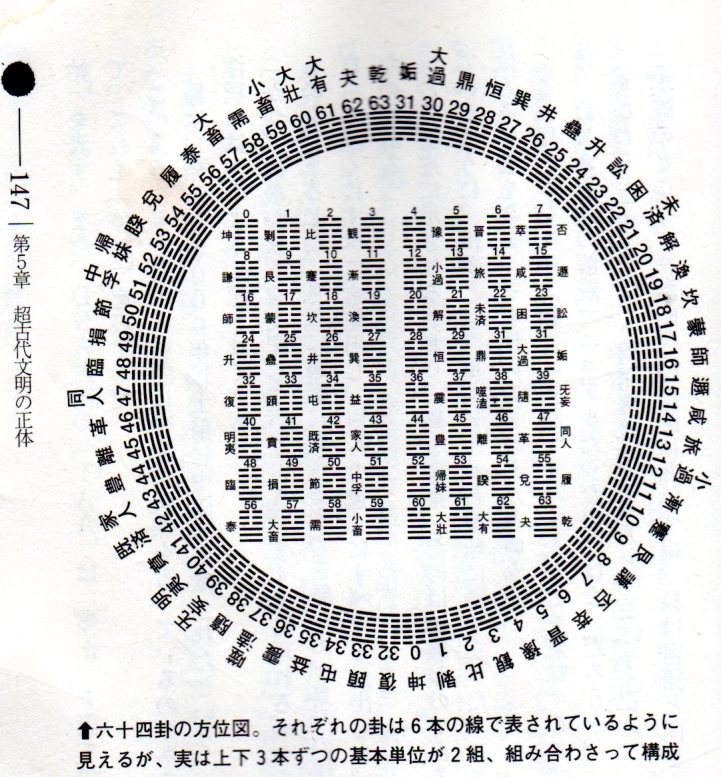
【表は、学研『ニビルの謎』より】
●はじめに
これは言うなれば、知的道楽のようなもの。
私自身、易経というものをほとんど知らない。
「当たるも八卦、当たらぬも八卦」という程度にしか、「八卦」のことを知らない。
そんな私が現在、八卦に興味をもっているのは、それがDNAと関係があるのではないか
という点に着目したから。
改めて、その謎解きに挑戦してみる。
ちょうど1年ぶりの再開である。
●2進数
私たちは日常生活の中では、10進数を使っている。
これは人間の指が10本であることに、大きく関係しているという。
これに対してたとえばコンピューターの世界などでは、2進数を使用する。
2進数というは、(0)と(1)だけの世界をいう。
(―)と(+)でもよい。
便宜上、10進数の(1)と(2)を使用する。
その2進数では、たとえばつぎのように数える。
(かっこ)内は、10進数による数え方をいう。【表1】
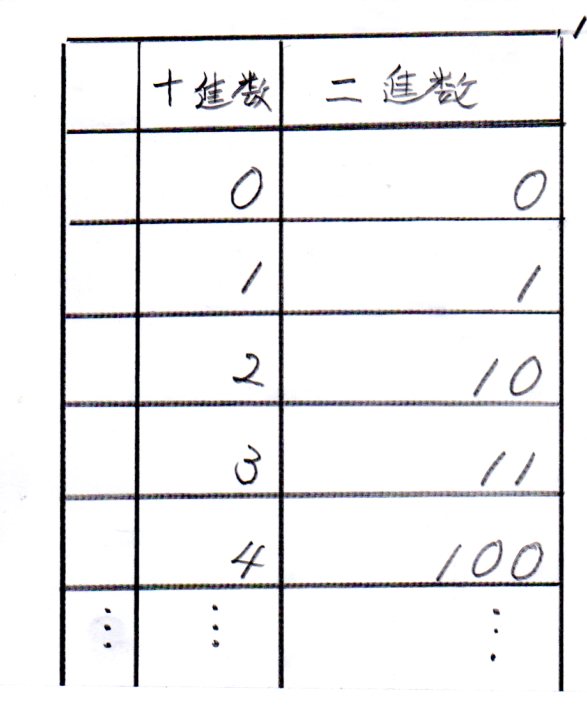
0(0)
1(1)
10(2)
11(3)
100(4)
101(5)
・
・
・
これでは数が大きくなるについて、段がついてしまうので、頭に(0)をつけ、わかり
やすくする。
つぎの表がそれである。
便宜上、6桁にしたが、それには理由がある。
その理由は、あとで述べる。
000000(0)
000001(1)
000010(2)
000011(3)
000100(4)
000101(5)
000110(6)
000111(7)
001000(8)
001001(9)
001010(10)
001011(11)
001100(12)
・
・
・
これですっきりした。
●八卦との関係
八卦では、一本の長い棒(-)と、二本の短い棒(・・)で、数を表す。
たとえば……、
(・・は、短い二本の棒、ーは、長い棒を表す。)【表2】
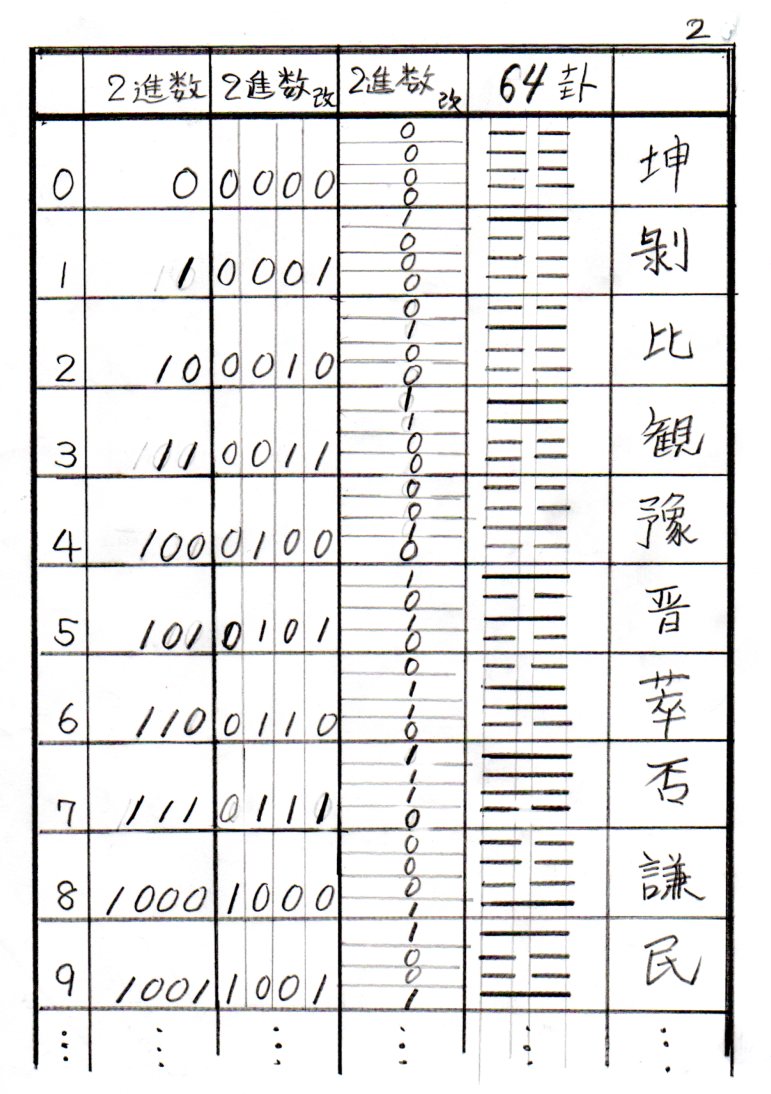
000000(0)⇒・・
・・
・・
000001(1)⇒―
・・
・・
000010(2)⇒・・
―
・・
000011(3)⇒―
―
・・
●長い棒と二本の短い棒
まずここで理解してほしいことは、八卦は、2進数で書かれた数字であるということ。
俗説によれば、伏義※という伝説上の賢者によって、発明されたという。
その当時の中国には、もちろん、数字の(0)(1)は、存在しなかった。
(中国語でいう漢字には、(0)の概念はない。)
だから(長い棒)と(二本の短い棒)で、「数」を表したとしても、何もおかしくない。
……というような回りくどい説明は、ここでは省略する。
八卦で使う(棒)は、二進数を表す。
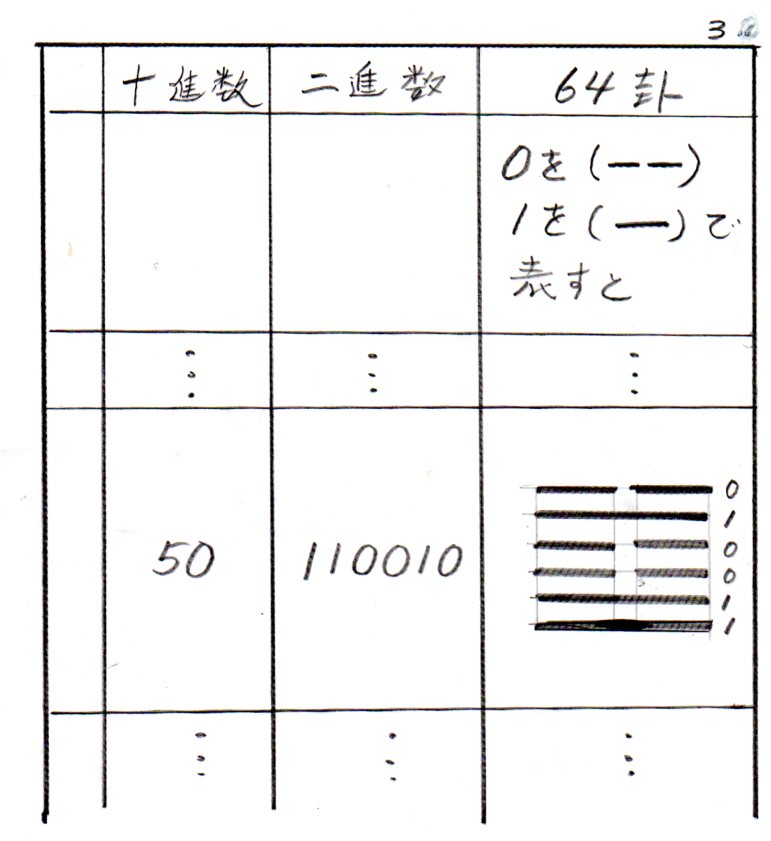
たとえば10進数の(50)は、2進数では「110010」となる。
それを2種類の棒で書き表すと、【表3】のようになる。
●DNA
同じようにDNAについての説明も省略する。
そのDNAは、4つの塩基(AGCT)から、3つの組み合わせで、構成される。
Aは「アデニン」、Gは「グァニン」、Cは「シトシン」、Tは「チミン」を表す。
その4つの中から、たとえばATCと3つが結合し、それが螺旋階段のように並び、DN
Aを構成する。
それを1個とするなら、人間のDNAは、約30億個あるとされる。
それはいわばコンピューターでいうプログラムのようなもの。
「設計図」と表現する人もいる。
この設計図に応じて、人間の「形」ができる。
●必要条件
そのDNAと八卦との不思議な関係については、すでに多くの研究家が本に書いている。
しかしDNAはDNA。
八卦は八卦。
それもそのはず、DNAは、戦後、発見された。
歴史は浅い。
八卦は、俗説に従えば、5500年前からあったという。
3000年前でも、2000年前でもよい。
この際、年代はどうでもよい。
少なくとも、DNAの発見は、ごく最近のもの。
八卦は、それよりもずっと昔からあった。
だからもし八卦がDNAの配列をうまく説明したとしても、それだけでは必要十分条件
を満たしたことにはならない。
偶然の一致ということも、ありえる。
が、ともかくも、その「必要条件」だけでも、ここで考えてみたい。
本当に、何らかの関係があるのか。
それともないのか。
(十分条件を満たすためには、その論理で、ほかの未知のDNAの構造まで説明しなけれ
ばならない。)
はたして八卦とDNAの間には、何かの関連性があるのだろうか。
●64卦
八卦では、64卦ともいうように、8x8=64の卦(け)を基本にものを考える。
そこで10進数でいう(0)を2進数で、(0000000)(6桁)とする。
(63)は、(111111)(6桁)となる。
最近のコンピューターは、64ビットマシンが主流。
そのことも記憶のどこかにとどめておいてほしい。
この6桁の数字を、(長い棒)と(短い2本の棒)で表したのが、八卦ということにな
る。
【64卦の方位図】
●DNA
先にも書いたように、DNAは、4つの塩基のうち、3つの塩基の組み合わせで、最小
単位を構成する。
「3文字言語」という言葉も、そこから生まれた。
そこでここでは、6桁の(棒)を、3組に分けてみる。
当然のことながら、2本ずつの3組になる。
(八卦をDNAに、無理にこじつけようとしている感じがしないでもないが、そこは許し
てほしい。)
が、ここでたいへん興味深い事実に気がつく。
(長い棒)と(短い2本の棒)の組み合わせは、4通り。
この4通りという数は、4つの塩基の数と、奇妙なことに一致する。
が、ここでは、まだ、偶然の一致ということにしておく。
つまりだからといって、八卦とDNAとの間に、何らかの関連性があるとは言えない。
ともかくも、4つの組み合わせ、つまりパターンができる。
それをここでは、パターン(1)(2)(3)(4)としておく。【図4】
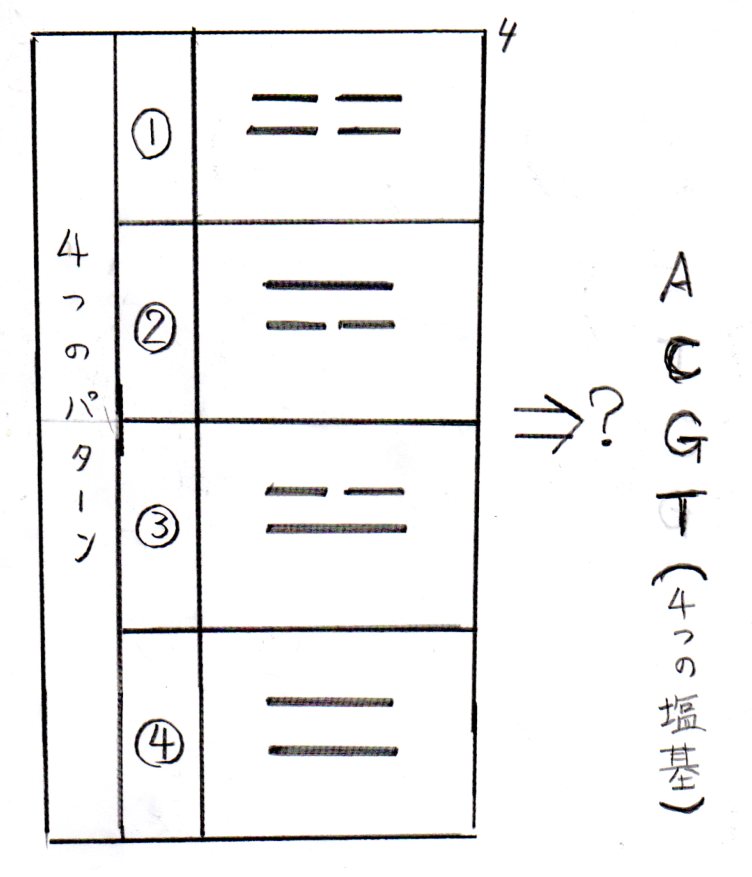
パターン(1)― ―
― ―
パターン(2)―――
― ―
パターン(3)― ―
―――
パターン(4)―――
―――【図4-2】
●10進数の(50)は、(110010)
こうして6桁の八卦を、3つに分解し、それぞれのパターンに、(1)(2)(3)(4)
と番号をふってみる。
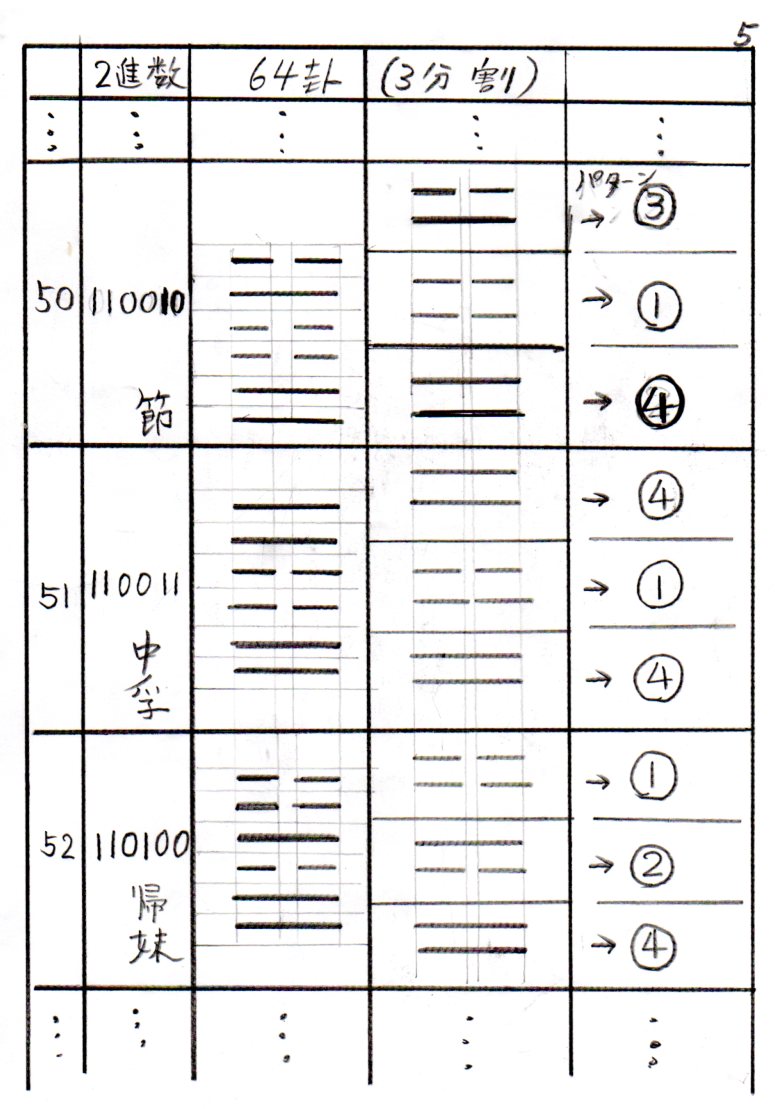
たとえば10進数の(50)は、2進数では(110010)となる。
これを3つの組に分けると、(11)(00)(10)となる。
が、八卦をよく見てもらうとわかるが、数字の並び方が逆になっている。
(50)は、(010011)となっている。
だから3つの組に分けると、(01)(00)(11)となる。
これを先にあげた、4つのパターンに当てはめてみる。
すると(50)は、(3)(1)(4)となる。
同じように、(51)は、(4)(1)(4)。
(52)は、(1)(2)(4)となる。【表5】
●AGCTの相性
ここで最初の難関は、DNAでいう4つの塩基と、ここでいう4つのパターンの間には、
何か関係があるのだろうか。
あるとすれば、DNAの4つの塩基、(AGCT)は、それぞれ4つのパターンのうち、
どれと同じと考えたらよいだろうか。
その関連性を解く鍵がひとつある。
それはDNAにおいては、4つの塩基の中から3つの塩基で最小単位を構成するが、それ
ぞれに相性というのがあるそうだ。
たとえば、「AはTとのみ結合し、GはCとのみ結合する」(「ニビルの謎」)とある。
(DNAについての勉強は、今始めたばかりなので、不正確で申し訳ない。)
●プラスとマイナス
そこでさらに仮定を飛躍させる。
今まで(長い棒)と(二本の短い棒)と書いてきた部分を、(+)と(-)に置き換えて
みる。
すると、ここで磁力的な説明がつくのがわかる。
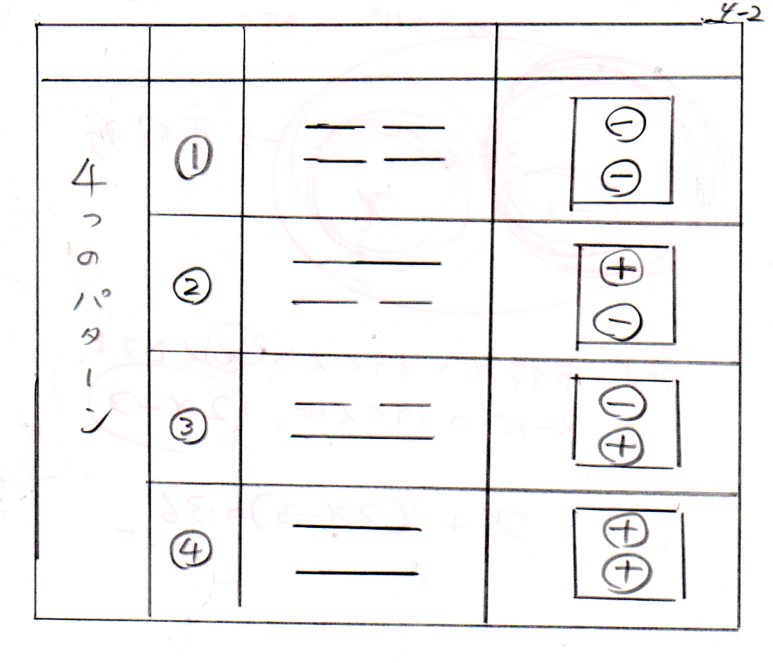
(短い棒を、マイナス、長い棒を、プラスとした。
もちろんその反対でもよい。)【図4-2】
パターン(1)は、(-)
(-)
パターン(2)は、(+)
(-)
パターン(3)は、(-)
(+)
パターン(4)は、(+)
(+)となる。
ここで電磁的にものを考えると、……どれとどれが結合すると考えてよいのか?
(+)と(-)は結合する。
(-)と(-)は結合しない。
つまりパターン(1)は、パターン(2)と(4)と結合する。
同じようにパターン(4)は、パターン(1)と(3)と結合する。
(+とーは、結合する。)
反対に考えると、パターン(2)は、パターン(4)のみとしか結合しない。
パターン(3)は、パターン(1)のみとしか結合しない。
つまり、パターン(2)は、Aもしくは、G。
パターン(3)は、Aもしくは、G、ということになる。
ここでパターン(2)をAと仮定すると、パターン(4)がTということになる。
すると、パターン(3)は、Gということになる。
残ったパターン(1)は、C!
もう一度、整理してみる。
パターン(2)をAと仮定すると、
パターン(1)=C
パターン(2)=A
パターン(3)=G
パターン(4)=T、ということになる。……仮定(1)
同じように、今度はパターン(2)をGと仮定すると、
パターン(1)=T
パターン(2)=G
パターン(3)=A
パターン(4)=C、ということになる。……仮定(2)
2つのケースが考えられる。
仮定(1)と仮定(2)はどちらが正しいのだろうか。
あとは実際のDNAの配列に当てはめて考えてみるしかない。
矛盾なく、合理的に説明できるほうが正しいということになる。
●塩基(3文字言語)
「ニビルの謎」に紹介されている、DNAの3文字言語を並べてみる。
「CGTAGAATTCT……」(P142)。
この並び方を合理的に説明するのは、(仮定1)のほうなのか。
それとも、(仮定2)のほうなのか。
?????
●DNA言語
では具体的に、10進数の(0)から(63)までを、DNAの3文字言語で置き換え
てみる。
ここでは前述(仮定1)に従って、並べてみる。
0……CCC
1……ACC
2……GCC
3……TCC
4……CAC
5……AAC、となる。
同じように、今度は前述(仮定2)に従って、並べてみる。
0……TTT
1……GTT
2……ATT
3……CTT
4……TGT
5……GGT、となる。
どちらが正しいのだろう?
頭の中を整理するため、10進数の(50)(51)(52)を、64卦で表し、さらに
それを3つのパターンに分けてみる。【図5】
八卦とDNAの間には、何か、関係があるのだろうか。
そこでもう一つのヒント。
DNA言語では、「TAA」は、「停止」を意味するという。
これはコンピューターでプログラムを組んだことがある人なら、みな知っていることだが、
プログラムの始めと終わりには、特殊な命令を入れる。
私はベーシック言語しか知らないが、ベーシックでは、「END」を書く。
その「END」に当たる言葉が、DNA言語では、「TAA」という。
この「TAA」を、(仮定1)で翻訳すると、「TAA」は、2進数で「11・10・1
0」となる。
10進数になおすと、「23」。
漢字では、「訟」。
数字を反対に並び替えると、「01・01・11」とすると、「58」。
漢字では、「需」。
今度は「TAA」を、(仮定2)で翻訳すると、「TAA」は、2進数で、「00・0
1・01」となる。
10進数になおすと、「40」。
漢字では、「明夷」。
数字を反対に並び替え、「10・10・00」とすると、「5」。
漢字では、「晋」。
整理してみる。
28……訟
58……需
40……明夷
5……晋
これら4つの漢字の中で、「END」を表すものがあれば、ビンゴー!
しかし残念ながら、「ニビルの謎」によれば、「END(停止)」を表すのは、「9」、
「ごん(「良」の上の点を取った文字)」だそうだ。
●今日はここまで
何か関係がありそうで、ない?
なさそうで、ある?
今日は、しかし、ここまで。
Time Up!
このつづきは、またの機会に書いてみたい。
が、これだけは覚えておいてほしい。
年代を特定するのはむずかしいが、古代中国では、何かとてつもない不思議なことが起き
ていた。
周囲文化とはかけ離れた、突出した科学が存在していた。
文中に書いた、「伏義(「義」の文字は現代漢字を使った)」にしても、調べれば調べる
ほど、不思議な人物(?)である。
興味のある人は、自分で調べてみてほしい。
(はやし浩司 家庭教育 育児 教育評論 幼児教育 子育て Hiroshi Hayashi 林浩司
BW はやし浩司 幼児教室 育児 教育論 Japan はやし浩司 DNA 八卦 易経
八卦の謎 謎の八卦 伏義 はやし浩司)
2011/11/16追記
【東洋医学(黄帝内経・素問)の謎】
こうした「八卦とDNAの関係」に興味をもったのには、理由がある。
私が書いた本の一部を、ここに紹介する。
(出典は、はやし浩司著『目で見る漢方診断』。
Hiroshi Hayashi++++++はやし浩司
●黄帝内経・地動説









●黄帝は実在したか?





Hiroshi Hayashi++++++Nov. 2011++++++はやし浩司・林浩司
【DNA情報は、64ビット言語で書かれたプログラム】byはやし浩司2011/11/16夜記
+++++++++++++++++++++++++++++
昨日(2011年11月15日)から、DNAについて考えている。
今日で2日目。
ド素人の、そのまたド素人の私が、DNAに興味をもっている。
きっかけは、八卦。
あの八卦は、実はDNA配列を説明したものという説に、興味をもった。
自分なりに検証してみようという気になった。
言うなれば、知的道楽。
で、今朝(2011/11/16)、つぎのような原稿を書いた。
前もって断っておくが、DNAを2進数で表そうとしているのは、世界でも私が最初だと
思う。
あちこちのサイトをのぞいてみたが、DNAを2進数で表した論文は、私が知るかぎりな
い。
だから、おもしろい。
……ということで、昨日、そして今朝につづいて、原稿のつづきを書いてみる。
+++++++++++++++++++++++++++++
●4つの塩基を、2進数で表してみる
昨日、4つの塩基を(ー)と(+)に置き換え、さらに2進数に置き換えるところまで
考えた。
この世界は、現在恐ろしく進歩していて、私がここに書いていることは、英語で言えば、
アルファベットのようなもの。
プロの人が読んだら、私のことを「アホ」と思うだろう。
が、だからといって、遠慮することはない。
私は私。
私の発想で、ものを考えてみる。
で、今朝、4つの塩基について、(-)(+)の置き換え方は2通りあると書いた。
(1)パターン(2)を「A」と仮定するばあい。
(2)パターン(2)を「G」と仮定するばあい。
それについて書いた部分を抜粋してみる。
『パターン(2)をAと仮定すると、
パターン(1)=C
パターン(2)=A
パターン(3)=G
パターン(4)=T、ということになる。……仮定(1)
同じように、今度はパターン(2)をGと仮定すると、
パターン(1)=T
パターン(2)=G
パターン(3)=A
パターン(4)=C、ということになる。……仮定(2)
2つのケースが考えられる。』と。
●遺伝子情報を、2進数で書き換えてみる
ここでいう「パターン」というのは、つぎの4つの組み合わせをいう。
パターン(1)は……(-)(-)
パターン(2)は……(+)(-)
パターン(3)は……(ー)(+)
パターン(4)は……(+)(+)。
ここでは(仮定1)に従って、
パターン(1)=C
パターン(2)=A
パターン(3)=G
パターン(4)=T、としてみる。
すると(C)(A)(G)(T)は、それぞれ、2進数で、つぎのように表せる。
C=(00)
A=(10)
G=(01)
T=(11)
この規則に従って、大腸菌の遺伝子を、2進数で表してみる。
どんなことになるだろうか。
●例題塩基配列:大腸菌由来 RNase HI 遺伝子
大腸菌の遺伝子配列(一部、4501~5041)は、つぎのようになっている。
4501 taaaaacaag ccacgaattc gccaggcggt tggagccacc cggcaatgtc gtaaaccaca
4561 ggcttaaact tcaacttggt agcctgtatc ttccagtgtg ggattcatcg ccgcggcacg
4621 agccagttca tcacagcgtt cgttttccgg gtgtccggca tggcctttaa cccattccca
4681 tttgatttga tgctgcccca atgcagcatc aagacgttgc cagagatcga cattttttac
4741 tggttttttg tctgcggttt tccagccacg ttttttccag ttatggatcc actgggtgat
4801 accctggcgg acatactggc tgtcggtact caaaatgact tcgcaatgtt cttttaacgc
4861 ctccagcgcg acaatagcgg ccatcaactc catacggttg ttggtggtgc gggtgtagcc
4921 agcgctaaag gttttctcgc gtccgcgata gcgtaaaata gcgccgtaac ccccaggtcc
4981 tggattgccc agacacgaac catcggtgaa aatttctacc tgtttaagca tctctggtag
5041 acttcctgta attgaatcga actgtaaaac gacaagtctg acataaatga ccgctatgag
以上の中の(4501)と(4561)だけを、2進数で置き換えてみる。
(何しろ数が膨大なので……。)
以下が、その結果である。
4501 (11)(10)(10)(10)(10)(10)(00)(10)(10)(01)
(00)(00)(10)(00)(01)(10)(10)(11)(11)(00)
(01)(00)(00)(10)(01)(01)(00)(01)(01)(11)
(11)(01)(01)(10)(01)(00)(00)(10)(00)(00)
(00)(01)(01)(00)(10)(10)(11)(01)(11)(00)
(01)(11)(10)(10)(10)(00)(00)(10)(00)(10)
4561 (01)(01)(00)(11)(11)(10)(10)(10)(00)(11)
(11)(00)(10)(10)(00)(11)(11)(01)(01)(11)
(10)(01)(00)(00)(11)(01)(11)(10)(11)(00)
(11)(11)(00)(00)(10)(01)(11)(01)(11)(01)
(01)(01)(10)(11)(11)(00)(10)(11)(00)(01)
(00)(00)(01)(00)(01)(01)(00)(10)(00)(01)
数字の羅列だけで、まったく意味がわからない。
そこで最初から、3組ずつ、まとめてみる。
全部はできないので、最初から3x10個だけにする。
(11)(10)(10)
(10)(10)(10)
(00)(10)(10)
(01)(00)(00)
(10)(00)(01)
(10)(10)(11)
(11)(00)(01)
(00)(00)(10)
(01)(01)(00)
(01)(01)(11)
これから(かっこ)を取り外してみる。
(111010)
(101010)
(001010)
(010000)
(100001)
(101011)
(110001)
(000010)
(010100)
(010111)
これらの数字を、今度は、10進法で書き改めてみる。
(111010)……58
(101010)……42
(001010)……10
(010000)……16
(100001)……33
(101011)……43
(110001)……49
(000010)…… 2
(010100)……20
(010111)……23
つぎに今度は、これらの10進法の数字に、八卦でいうところの漢字をあてはめてみる。
(111010)……58(需)
(101010)……42(既済)
(001010)……10(蹇)
(010000)……16(師)
(100001)……33(頣)
(101011)……43(家人)
(110001)……49(損)
(000010)…… 2(比)
(010100)……20(解)
(010111)……23(訟)
その「END」に当たる言葉が、DNA言語では、「TAA」という。
この遺伝子配列の中では、冒頭にそれがあるのがわかる。
「TAA」は、2進法配列では、(111010)。
10進法に改めると、58、つまり漢字では、「需」。
この「需」というのは、どういう意味なのだろう。
『漢字牧場サイト』では、つぎのように説明する。
『……「需」の復習ですが、巫祝が雨乞いをすることを「需」といいます。そして、その
雨乞いをする巫祝のことを「儒」というのです』(「漢字牧場」より)と。
念のため八卦の表現方法にするため、「(111010)……58(需)」の数字を、逆に
並びかえてみる。
(111010)は、(010111)となる。
これを10進法に改めると、23(訟)となる。
Goo辞書には、「訟……裁判で是非を争う。訴える」(Goo辞書)とある。
「需」も「訟」も、意味の上においては、DNAの3言語の意味とはつながらない?
もしここで「スタート」を表す漢字とつながれば、私は飛び上がって喜んだだろう。
八卦は、DNA言語の意味と一致した!、と。
しかしそういうことは、なさそうだ。
(ガッカリ……。)
が、ここでへこたれてはいけない。
この世界は、先にも書いたように、底なしに深い。
とにかく今夜はここまで。
おもしろかった。
楽しかった。
明日からもまた、DNAについて考えてみたい。
(はやし浩司 家庭教育 育児 教育評論 幼児教育 子育て Hiroshi Hayashi 林浩司
BW はやし浩司 幼児教室 育児 教育論 Japan はやし浩司 DNA言語と二進数 2進
数 DNA 2進数論 八卦とDNA 3文字言語 DNA言語 2進数 易経 八卦)
Hiroshi Hayashi++++++Nov. 2011++++++はやし浩司・林浩司
【3】(近ごろ、あれこれ)□□□□□□□□□□□□□□□□□□□□□□□□□□
休みます。
☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
はやし浩司のホームページ http://www2.wbs.ne.jp/~hhayashi/
☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
***********************************
このマガジンがお役にたてそうな人が、あなたのまわりにいませんか?
よろしかったら、どうか、このマガジンのことを、お友だちの方に
話していただけませんか?
よろしくお願いします。 はやし浩司
***********************************
■■■■■■■■■■■■■■■■■■■■■■■■
まぐまぐプレミア版(有料版)のお申し込みは……
http://www2.wbs.ne.jp/~hhayashi/page141.html
■■■■■■■■■■■■■■■■■■■■■■■■
. *※※
.※※ ***※
.*※※…※}※**
. **++ ※))
. {※}※※ /
. ※*… /mQQQm
.**/| |Q ⌒ ⌒ Q Bye!
. = | QQ ∩ ∩ QQ
. m\ ▽ /m~= ○
. ○ ~~~\\//
.=================================
.みなさん、次号で、またお会いしましょう!
.=================================


<< Home