(3)イースター島の謎byはやし浩司
【謎のイースター島】
●V3までのダイジェスト版(ガイド版)です。
まず、このビデオをご覧ください。
内容をより深く理解していただけます。
●形状の秘密
この図は、UFO」ではない。
グーグルアースの写真を、そのまま転載したもの。
が、このタイプのUFOは、世界各地で目撃されている。

(UFOに見えるイースター島)
で、これが、イースター島。
ほぼ左右対称の形をしている。
そこでそれを確かめるため、つぎの作業をしてみた。
まずつぎの地図(ウィキペディア百科事典)をコピーする。
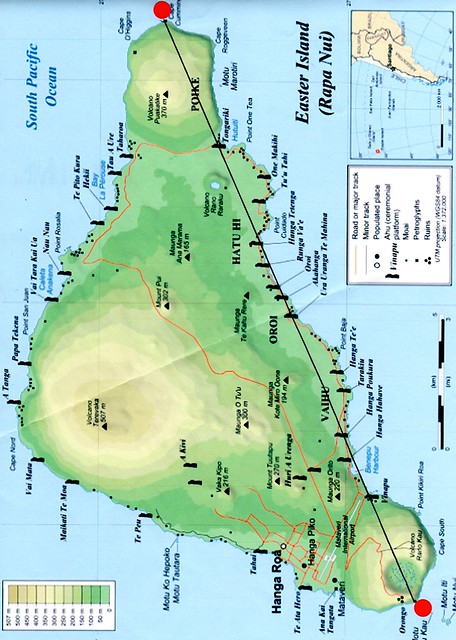
(イースター島の地図、印刷の関係で、左へ90度回転してある。)
左下(写真では、真下の赤部分)の円形の火山を、A火山とする。
右下の円形の火山を、B火山とする。
これらA火山の左端、B火山の右端を、そろえて、そこで2つに折ってみる。
それをわかりやすくするため、図の中の両端の先端部に、赤いシールを張っておいた。
すると不思議なことに、イースター島は、きれいに2つに分けらることがわかった。
しかも折り目の先端部(青いシール)は、同時にイースター島の最先端部の位置と、一致する。
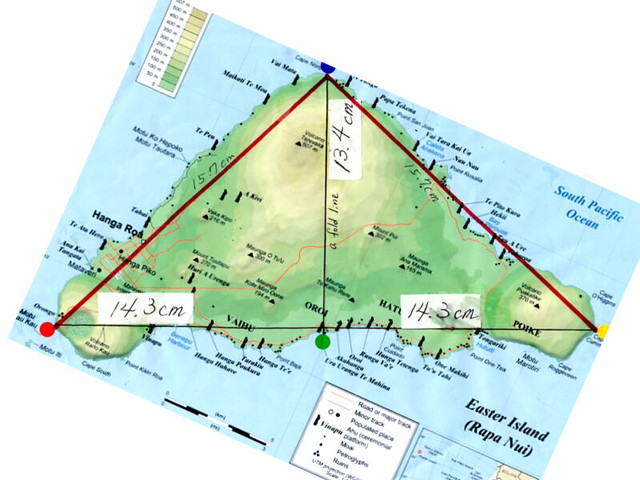
2辺の斜辺の長さを測るまでもなく、イースター島は、「正確な二等辺三角形」になっている!(はやし浩司説)
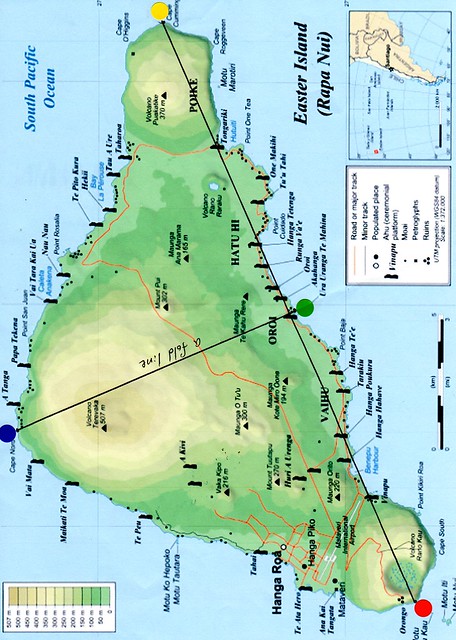
(2つに折り、折り目にラインを入れてみた)
そこで寸法を正確に測定してみる。
その測定した結果が、つぎの図である。
実際の距離は、グーグルアースを使えば、センチ単位まで正確に測定することができる。
が、ここでは簡単に、プリントアウトした図の上で、測定してみる。
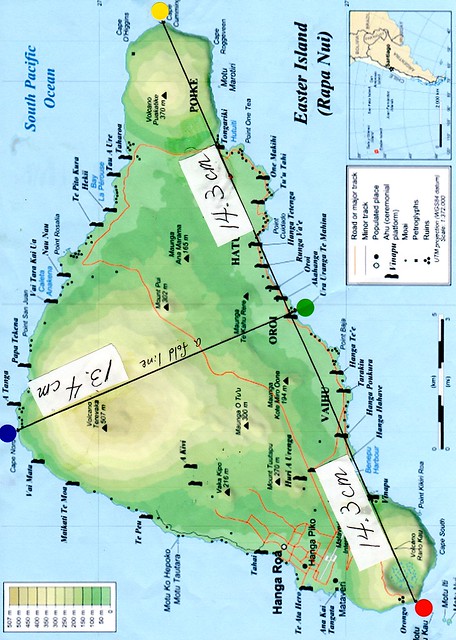
(測定結果を入れた、イースター島)
●直角二等辺三角形
が、これに驚いていてはいけない。
イースター島は、左右に対称な島である。
A火山(火山と言っても、この10万年近くは活動していない)と、B火山の端をよく見てほしい。
ちょうど、子どものへそのように、小さく飛び出た部分がある。
今回は、この(飛び出た部分)を測定の基準とした。
その(へそ部)と頂点にあたる(北端部)をつないでみた。
そしてできた形は、直角二等辺三角形。
(地図上では、92~3度になっている。)
(これを直角二等辺三角形と言わずして、何という?)
今まで、こうした視点で、イースター島を見た学者がひとりもいないというのも、驚くべきことと言ってよい。
言うまでもなく、この(事実)を発見したのは、私、はやし浩司である。
(オホン!)
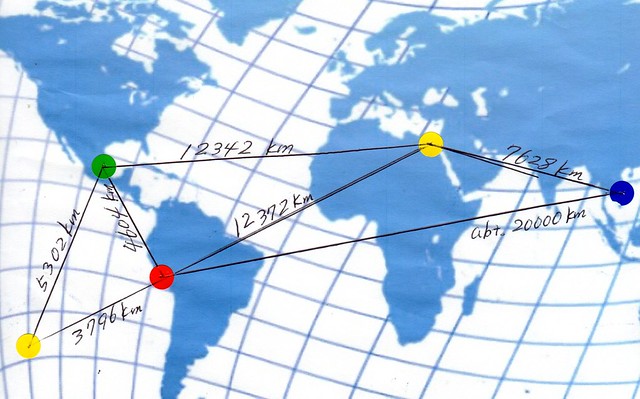
●実測値
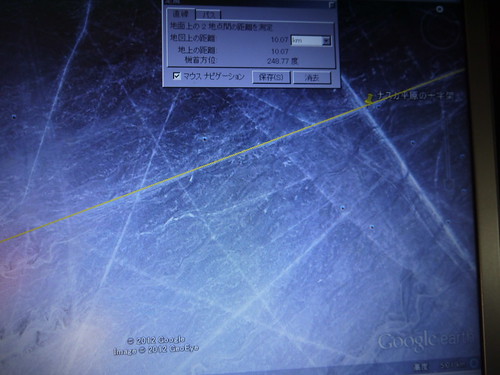
グールルアースの機能を使い、長さを実測してみた。
北端→西端……15927メートル(1)
西端→東端……23565メートル(2)
東端→北端……16574メートル(3)
(1)と(3)の値は同じはずだが、ここでは、北端部を三角形の頂点とした。
そのため、値が少しずれている。
これで計算してみると……
(手元に、タンジェントを計算する計算機がないので……。)
(1)15927の2乗=253669329
(2)23565の2乗=555309225
(3)16574の2乗=274697476
ここで(1)+(2)=(3)になれば、三平方の定理により、頂点は直角ということになる。
(もちろん有効数字の問題もあるので、こまかい数字には意味はないが……。)
(1)+(2)=528366805
正確に直角ではないが、やはり「ほぼ直角」という数値が出てきた。
「イースター島は、直角二等辺三角形の島である」と、断言してよい数値である。
●ダメ押し
ここまで書いても、まだ懐疑的な人がいるかもしれない。
「はやしの言っていることは、こじつけに過ぎない!」と。
が、つぎの事実を知ったら、あなたも、驚愕せずには、おれないだろう。
百聞は一見に如かずともいう。
2枚の写真を見比べてみてほしい。

(イースター島の地図)

(エジプトのピラミッド)

(イースター島とピラミッドの比較)
そこでラフな計算だが、イースター島の(高さ)を(底辺の長さ)で割ってみる。
(1)0・4685という数字が出てきた(注:もともとの数字が、不正確)。
(13・4÷28・6=0・4685)
エジプトのピラミッドのうち、最大のものであるクフ王のピラミッドは、『ピラミッド建築の頂点とされ、最大規模を誇る。現在高さ138.74m(もとの高さ146.59m)、底辺:230.37m』(ウィキペディア百科事典)と。
このクフ王のピラミッドの(もとの高さ)を(底辺の長さ)で割ってみる。
(2)0・6363という数字が出てきた(146・59÷230・37にて計算)。
「0・47」と「0・63」。
最初に測ったイースター島の寸法が、この図でもわかるように、大ざっぱなものである。
それを考慮に入れても、値がちがいすぎる。
しかし見た感じ、イースター島の形とピラミッドの形は似ている。
なぜか。
理由は簡単。
ピラミッドは、真正面からではなく、斜め方向から見ている。
そのため坂がなだらかに見える。
私たちはピラミッドというと、真正面から見た三角形のピラミッドを想像する。
が、真正面ではなく、45度、ななめの方向から見たら、どうなるか。
ピラミッドの縦線が一本入るため、そのほうが、縦線が垂直であることから、ピラミッドの大きさを正確に見ることができる。
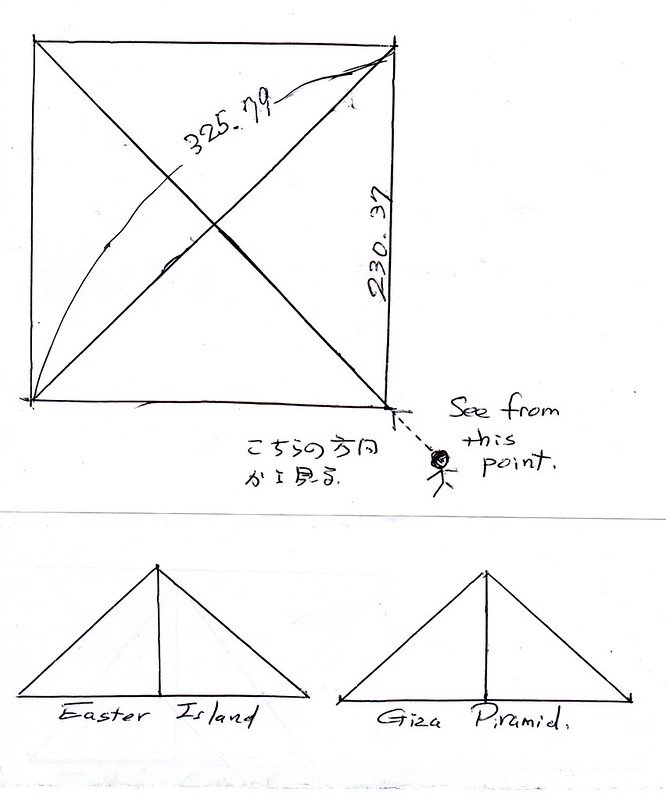
(ピラミッドを斜め45度の角度から見ると、どうなるか? それを示したのがこの図。この図でもわかるように、イースター島と、ピラミッドは、形の上において、区別がつかないほど、よく似ている。)
この角度で遠方から見ると、底辺の長さは、325・79(146・56x1/4142=325・79)メートルとなる。
この数字で、高さ146・56メートルを割ると、
146・56÷325・79=0・44990……という数字が出てくる。
「0・47」(イースター島)と、「0・45」(ピラミッド)!
(念には念を入れ、イースター島の実測値で計算してみる。
グーグルアースを使い、高さ(11198メートル)を、底辺(23551メートル)で割ってみる。
その値は、11198÷23551=0・4754=0・48。)
つまりイースター島の形は、エジプトのピラミッドを45度、斜め方向から見た形と、同じということになる!(はやし浩司説)
●イースター島は人工島?
こうしたイースター島ができた理由として、2つのことが考えられる。
(1)きわめて偶然に、このような形の島ができた。
(2)もとはある程度三角形の島だったが、整地(削ったり)したりして、現在の形になった。
(当然、その後、波によって浸食され、形は多少、変わった。)
あなたはどちらを信ずるか?
多くの人は、こう言うだろう。
「バカな! 偶然に決まっている!」と。
もしあなたが、懐疑派なら、もう少し先まで読んでみてほしい。
●モアイの謎
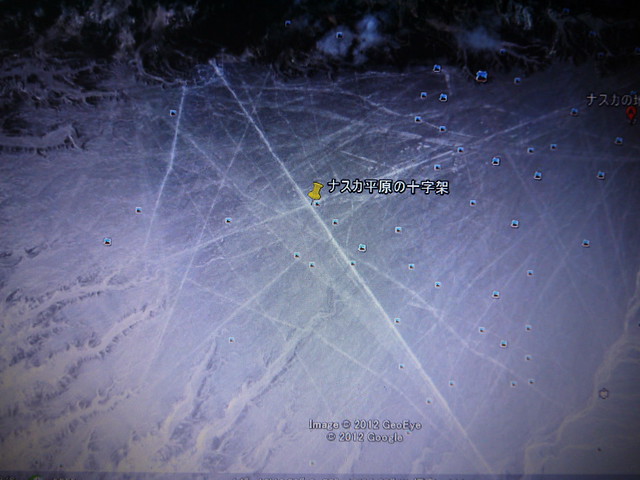
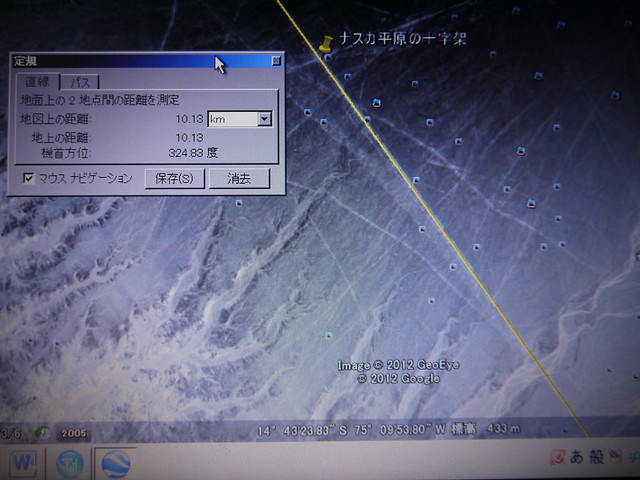
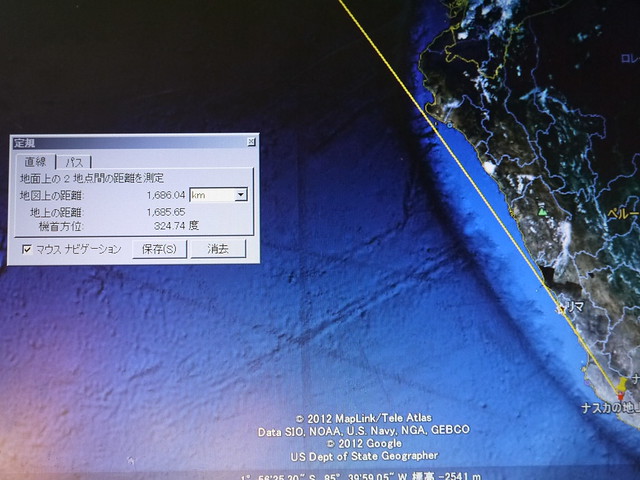
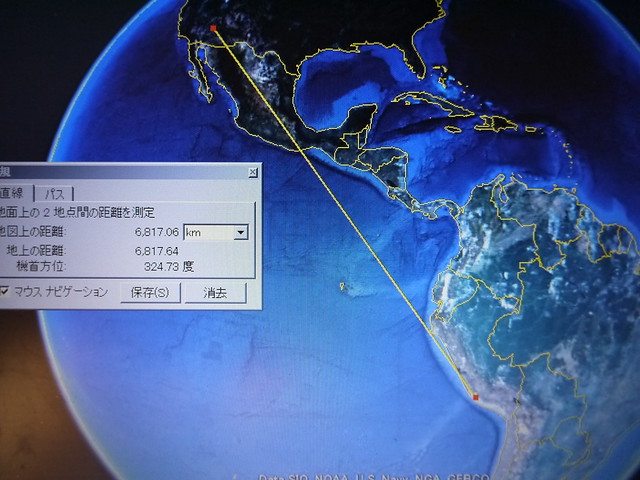
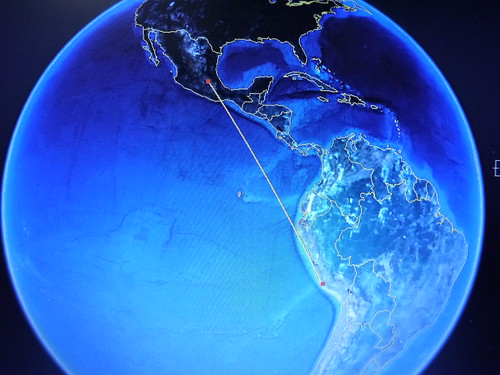
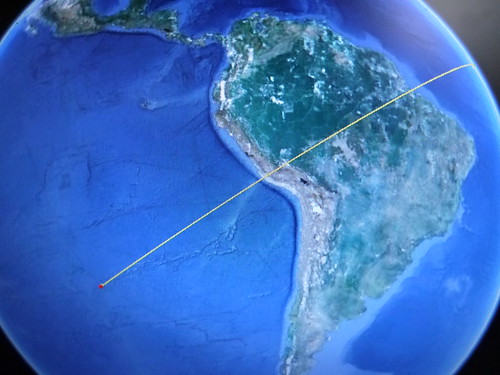
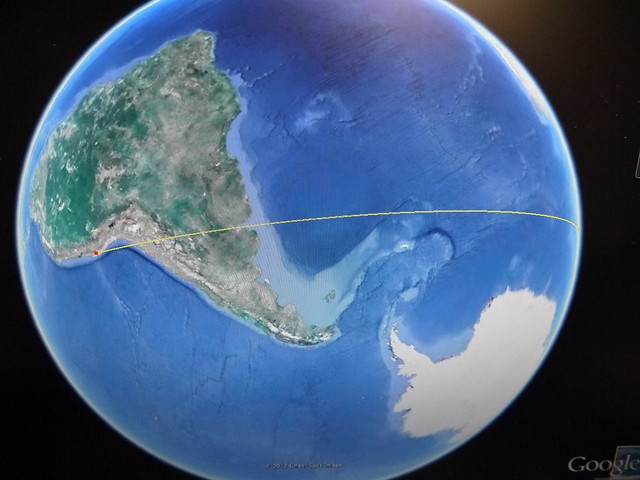
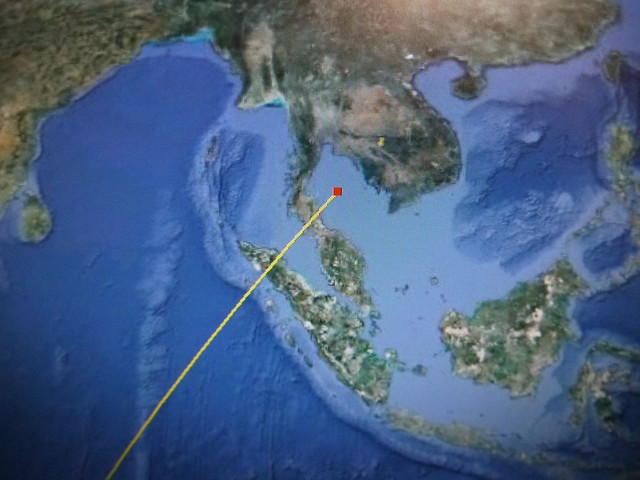
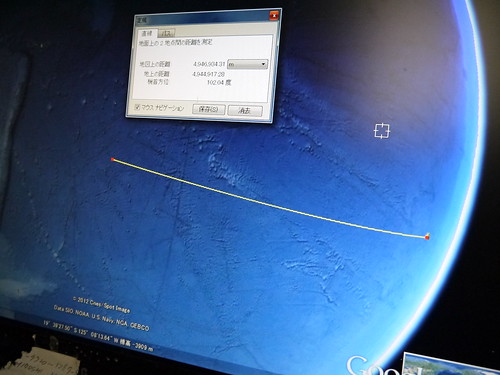
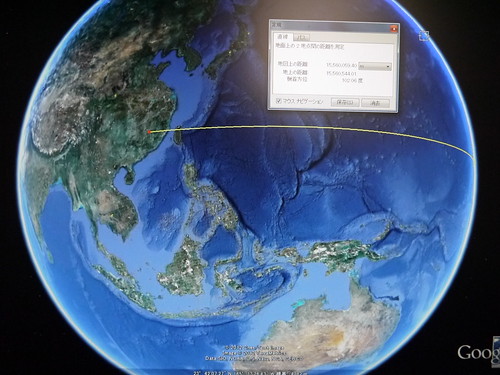
ナスカ(大十字架の交点)からイースター島(トロバカ山の山頂)まで、一本の直線を引いてみた。
この直線は、その先で、エジプトの3大ピラミッド(以下、ギザと表示)につながっている。
つまりイースター島とナスカ、それにギザは、一本の真直線でつながっている。
それはさておき、イースター島の中にその直線を走らせてみた。
ところが、である。
その直線とぴったりと重なるモアイ像があることがわかった。
しかもトロバカ山の山頂から見て、まさにナスカの方向に、である。
Catete Anakona(カテテ・アナコナ)湾の波打ち際にある、「Nau Nau(ナウナウ)」というモアイ像が、それである。
(なおこの直線は、ナスカの大十字架と、イースター島のトロバカ山(507メートル)の頂上を結んだ直線である。
日本人の私たちには、「トロ・バカ」とは、きわめて辛らつな名前に聞こえる。
これは余談だが、それだけに一度聞いたら、この名前は忘れない。)
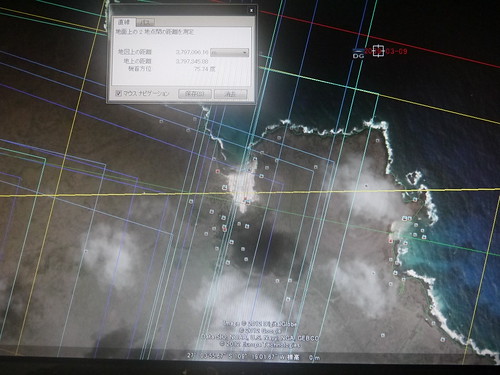
(黄色の線は、イースター島のトロバカ山の山頂と、ナスカの大十字架を結んだ線)

(白い部分は、砂浜。黄色の線の下に、点々とモアイが見えるのがわかる。これがナウナウ・モアイである。)
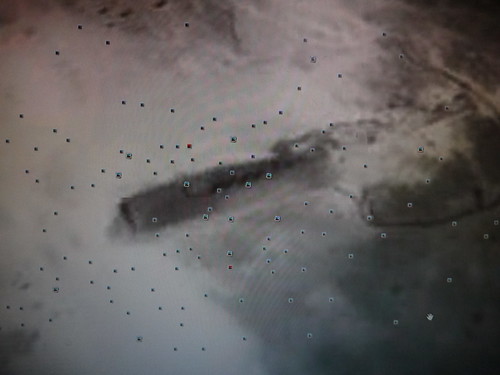

(グーグル・アース上で、ナウナウ・モアイをさがしてみた。)

(モアイ、「ナウ・ナウ」の写真。従来、モアイの顔が、方向を示していると考えられていたが、顔の方向ではなく、「並び方」である。並び方が、方向を示している。またそう考えると、モアイ像の謎が解ける。はやし浩司説)
●重大な発見
かねてから、モアイ像は、「どこかの方向を示している」と考えられている。
しかしその謎を解いた人はいない。
それもそのはず、モアイ像そのものが「方向」を示しているのではなく、その並び方が、方向を示している。(はやし浩司説)
このことは、空港の誘導灯を思い出してみれば、容易に理解できるはず。
まただからこそ、モアイ像は、何体も、並んで立っているということになる。
(はやし浩司説)
この一例だけで、そういう仮説を立てることは危険なことである。
それはわかっているが、解けない謎なら、思い切って発想を変えてみる。
ときには、そういう冒険も必要である。
ただとても残念なことに、前にも書いたように、日本のどこかの建設会社が、倒れていたモアイ像を、重機を使い、立てなおしてしまった。
日本の、だぞ!
お馬鹿というか、お節介というか!
専門の考古学者が、その場で立ち会ったのか?
どうしてナスカ平原を、ユンボで整地するような愚かなことをしてしまったのか?
イースター島の山の名前は、「トロ・バカ山」。
今となっては、仮に正確に立てられたとしても、学問的な信頼性は、ゼロということになる。
が、あきらめてはいけない。
ほかにも台座が残っているところがある。
●台座
そこでグーグルアースを使い、台座を探してみる。
わかりやすくするため、イースター島の北端にある付近の台座を探してみる。
台座なら、こうした上空からでも、探しやすい。

(イースター島の北端、やや東よりのあたり。)

(方向がわかりやすい台座。現在は、遺跡としてでしか、残っていないようだ。)

(その台座の示す方向を、右方向(東方向)に延長してみる。方向は、機首角を見ながら決めるので、きわめて正確に知ることができる。)

(直線を延長し、やってきたのが、このあたり。)

(今度は、別の台座を探し、左方向(西方向)に延長してみることにする。方向がしっかりと把握できる台座を選んだ。この台座も廃墟となっているよう。)

これらの方向の先に、何があるのか、今の時点ではよくわからない。
古代文明といっても、各地に散らばっている。
廃墟となり、さらに形すらも残っていないところもある。
あえて言えば、中国の長江方面を指しているのが、わかる。
●イースター島の謎
このようにイースター島の謎は、底なしに深い。
が、その「謎」も、視点を地上ではなく、空中に置いてみると、氷解する。
空中を自由に飛び回る人の視点で見ると、よくわかる。
イースター島は、遠く、宇宙の果てからやってきた人たちが、最初に降り立った島である?
つまり標識?
自分たちの乗り物の形に合わせて作った標識?
その標識には、さらにそれぞれの位置を示す標識を並べた?
それがモアイ像?
ならば現代の人間が使うようなナビゲート・システムを使わなかったかと、疑問に思う人もいるかもしれない。
しかし彼らは、もっと手っ取り早い方法を選んだ。
ちょうど登山家が、自分たちの歩いた道に石を積むように、あちこちに石を積んだ?
どういう人たちで、どういう技術をもった人たちかは、わからない。
しかしこと、土木工事に関しては、きわめて高度な技術をもった人たちである?
そこらの衛星をくりぬいて、自分たちの住居とすることくらいなら、朝飯前?
そんな人たちである?
もちろんここに書いたことは、SF小説レベルの話。
しかし「謎だ」「謎だ」と、無理な説明をこじつけるのも、そろそろ限界に来ているのではないか。
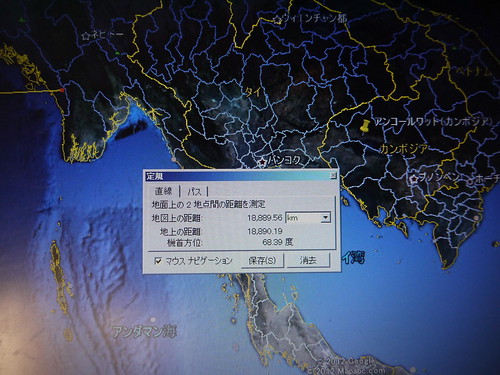
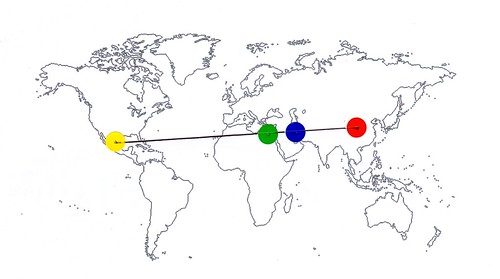
でないというのなら、なぜ(イースター島)と(ナスカの地上絵)、さらに(エジプトの三大ピラミッド)が、真一直線に並んでいるのか。
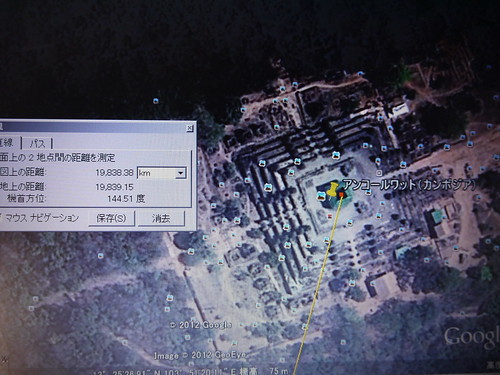
(その先では、アンコールワットにもつながっている、。)
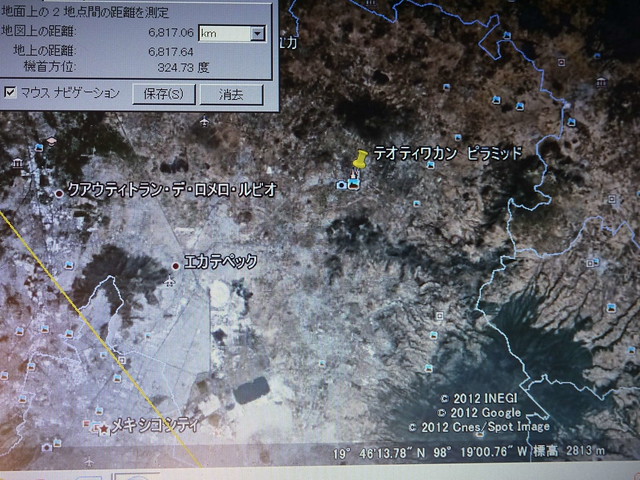
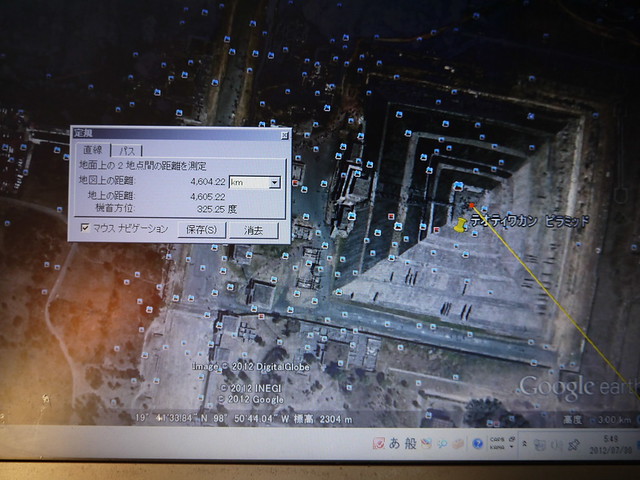
さらにナスカの大十字架(地上からは、何も見えない、幅200メートルの線)が、北は、テオティワカンの遺跡(メキシコ)を示し、南はアンコールワットの遺跡を示しているのか。
つまり(テオティワカンの遺跡)と(ナスカの大十字架)、さらには(アンコールワットの遺跡)は、真一直線に並んでいるのか。
「偶然の一致」という言葉を使うのも、ふつうの学者なら、もうそろそろ疲れるはず。
どうだろう。
このあたりで一度、発想を変えてみたら?
……ということで、今回「イースター島の謎」について、書いてみた。
(はやし浩司 イースター島の謎 モアイの謎 UFOの形をしたイースター島 家庭教育 育児 教育評論 幼児教育 子育て Hiroshi Hayashi 林浩司 BW はやし浩司 幼児教室 育児 教育論 Japan はやし浩司 Easter Island Moai Mystery of Easter Island)
Hiroshi Hayashi+++++++July. 2012++++++はやし浩司・林浩司